Pericyclic Reactions

Selection Rules and Orbital Symmetry

1. Cycloadditions exemplified
   1. Allyl cation with alkene: [π2s + π2s]
   2. Allyl anion with alkene: [π4s + π2s]
   3. Allyl cation with diene: [π4s + π2s]
   4. Triene with diene: [π6s + π4s]
   5. Tetraene with alkene: [π8s + π2s]
   6. One of a kind: [π14a + π2s]
2. Electrocyclic reactions: A formal introduction
3. Orbital correlation diagrams and the conservation of orbital symmetry
   1. The interconversion of 1,3-butadiene and cyclobutene
   2. The interconversion of 1,3Z,5-hexatriene and 1,3-cyclohexadiene

1 Cycloadditions exemplified

In a previous section we became familiar with the terminology of cycloadditions and the selection rules for 'symmetry allowed' and 'symmetry forbidden' reactions, based on the properties of FMOs. We will now take a look at the way these work in practice.

1.1 Allyl cation with alkene: [π2s + π2s]

This is a 4-electron (i.e. 4n) combination. The possible HOMO-LUMO combinations are mismatched, so a concerted supra-supra reaction is 'forbidden.'

×

1.2 Allyl anion with alkene: [π4s + π2s]

This is a 6-electron (i.e. 4n + 2) combination, so the HOMO-LUMO combinations are now matched for a concerted supra-supra process. Although such reactions are 'allowed,' the conditions can make it difficult to prove that they are not stepwise in nature (030 is probably concerted). Note that the dominant interaction is of the HOMO of the nucleophile (electron-donor) and the LUMO of the electron-acceptor component.

×

×

1.3 Allyl cation with diene: [π4s + π2s]

This is another 4n + 2 combination with the HOMO-LUMO pairs matched for a concerted supra-supra process. In example 032 the cation is made from the corresponding iodoalkene by treatment with a silver salt.

×

×

1.4 Triene with diene: [π6s + π4s]

This is a 10-electron (i.e. 4n + 2) combination, so the HOMO-LUMO combinations are matched for a concerted supra-supra process. In example 024 the π components are both cyclic, and therefore 'locked' in the conformation required for reaction.

×

×

1.5 Tetraene with alkene: [π8s + π2s]

This 10-electron (i.e. 4n + 2) combination is highly uncommon, but the orbitals are correctly matched for a concerted supra-supra process. In example 031 the reaction again benefits from the tetraene being 'locked' in the conformation required for reaction.

×

×

1.6 One of a kind: [π14a + π2s]

This 16-electron (i.e. 4n) combination is unique. For concerted bonding the orbital symmetry requirement is for one of the π systems to react anatarafacially and the other to react suprafacially. For 023 it was shown (by X-ray crystallography) that the antarafacial reactant is the 14π system, heptafulvalene. Models confirm that heptafulvalene is not flat, and it is evident that the conformational requirements of the [π14a + π2s] reaction allow it to compete successfully with the various alternative [π4s + π2s] and [π8s + π2s] cycloaddition modes that are also possible.

×

×

2 Electrocyclic reactions: A formal introduction

Electrocyclic reactions are pericyclic reactions in which a ring is formed or broken. We will analyse one specific case in detail — in pericyclic reactions once you know how to analyse one specific case of a particular reaction type, predicting the others is generally easy. It is also easier to understand a thermal reaction using the familiar HOMO rather than that of the excited state. Should a reaction turn out to be thermally forbidden, then it will be photochemically allowed.

×

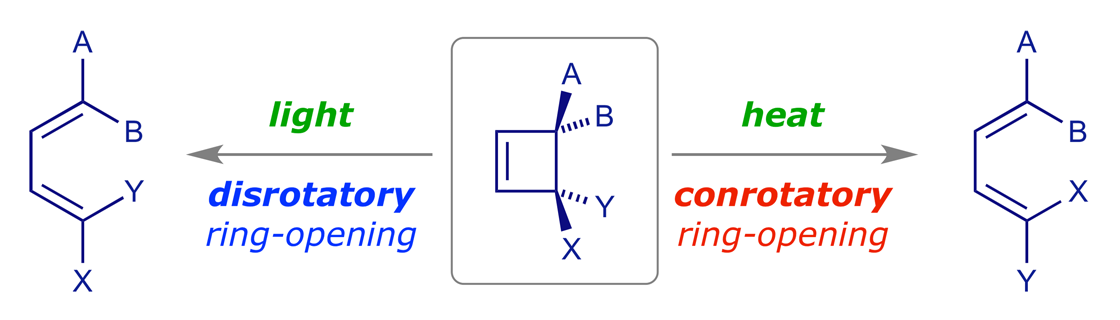
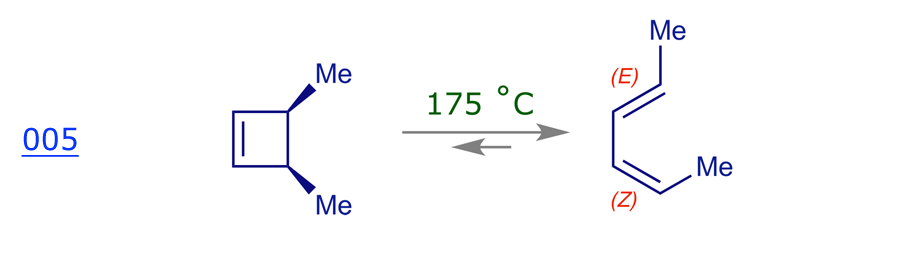
Recall that pericyclic reactions are reversible, and as this is a thermal reaction we expect the ring-opened diene to be favored because a cyclobutene ring is quite strained. However, it does not matter which reaction we use for our mechanistic analysis — ring-opening or ring-closure — as we must get the same result. The thermolysis of cis-3,4-dimethylcyclobutene has been thoroughly studied and it is stereospecific: the sole product is (E,Z)-2,4-hexadiene.

×

If we analyse the product we can immediately see the reason for this selectivity. There's only one reacting component, so we don't have to worry about a HOMO–LUMO pair. We simply use the HOMO of the diene. In the ring-closure reaction the terminal p orbitals must combine to give a bonding sigma orbital, so this must involve in-phase overlap. The only way we can achieve this is to rotate them either both clockwise or both counterclockwise. When they rotate in the same sense, the process is classified as conrotatory.

×

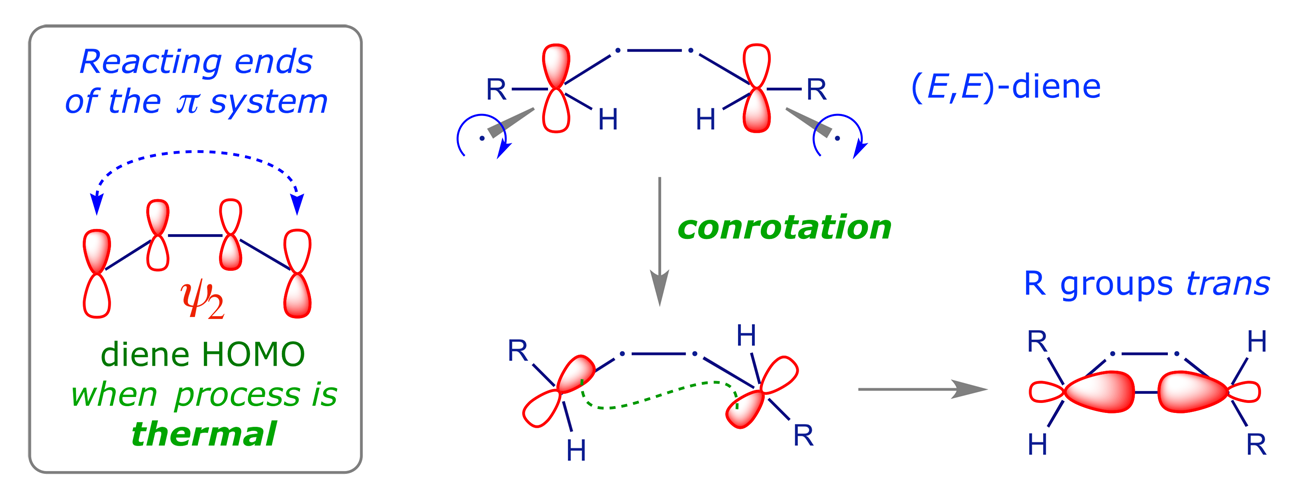
The scheme above shows only the π orbitals whose overlap create the C(3)–C(4) σ-bond of the cyclobutene. A complete analysis of the electrocyclic process will reveal how the other orbitals of the starting material are transformed into those of the product, and provides us with an opportunity to see the Woodward-Hoffmann approach to pericyclic reactions in operation.

3 Orbital correlation diagrams and the conservation of orbital symmetry

The selection rules for cycloadditions based on the electron count, previously discussed here, provide a means of predicting whether a concerted supra-supra cycloaddition is allowed or forbidden. A more fundamental principle — the conservation of orbital symmetry — underpins all pericyclic reaction pathways and was articulated in the 1960s by R. B. Woodward and R. Hoffmann, who described a series of detailed analyses from which the Woodward-Hoffmann rules emerged. The IUPAC definition of this fundamental principle is as follows:  Conservation of orbital symmetry requires the transformation of the molecular orbitals of reactants into those of products to proceed continuously by following a reaction path along which the symmetry of these orbitals remains unchanged.  We will see what this means for the cyclobutene-butadiene electrocyclic reaction. The analytical sequence can be summarised thus:

1. Identify any symmetry elements that are maintained throughout the course of the reaction.
2. List the orbitals in the usual order of increasing energy.
3. Draw the orbitals so as to show the signs of the coefficients.
4. Classify each of the orbitals with respect to the symmetry element.
5. Construct the correlation diagram following the principle that each orbital in the starting material must feed into an orbital of the same symmetry in the product.
6. Connect the orbitals of the starting material to those in the product that are the closest in energy and of the same symmetry.

3.1 The interconversion of 1,3-butadiene and cyclobutene

×

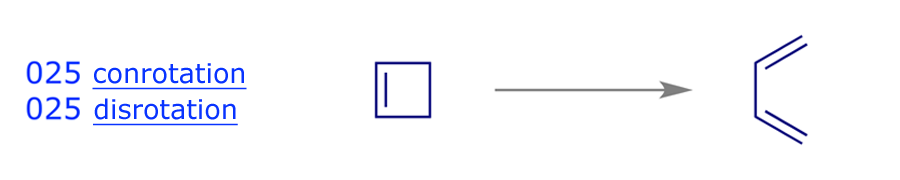
The FMO analysis in Section 2 indicates that the thermal electrocyclic ring-opening of cyclobutene will proceed by conrotation, which preserves a C₂ axis of symmetry (running through the centres of the σ and π bonds) during the reaction. This is the symmetry element chosen in the first of steps 1–6 above, and it is an easy matter to classify each orbital in the diagram below according to its relationship with the C₂ axis: if the structure is unchanged after rotation through 180° then it is symmetric (S), otherwise it is antisymmetric (A). The symmetry correlation diagram for cyclobutene conrotation (below) indicates that this ring-opening mode is allowed, i.e. there are no symmetry-imposed energy barriers.

×

A symmetry correlation diagram for cyclobutene disrotation can also be constructed, but this time the symmetry element maintained during the reaction is a mirror plane. The S/A correlations now have the π orbital of the cyclobutene evolving into the antibonding ψ₃ orbital of the diene, which would render the thermal disrotation symmetry forbidden. However, under UV irradiation, which can induce the promotion of an electron to the next level, the reaction is allowed to proceed by disrotation. With one electron in the former LUMO of the starting material, as shown in the correlation diagram below, the disrotatory process is energetically neutral and therefore allowed (N.B. for the photochemical reaction, ring closure is favoured).

×

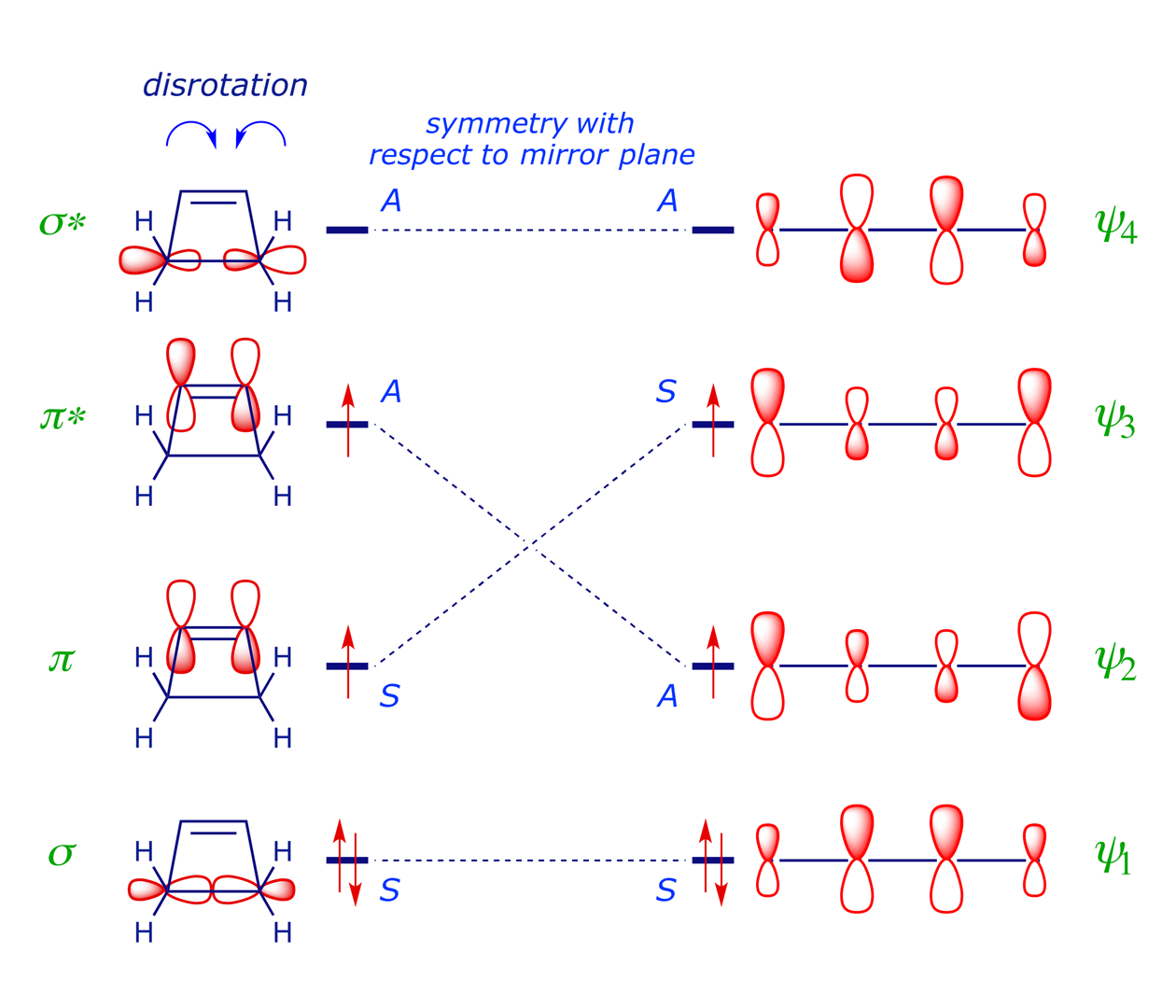
Note that the FMO approach, analysing only the HOMO of the diene in order to determine which rotation mode will give σ-bonding overlap, provides exactly the same prediction. The stereochemical outcome of a 4π disrotatory process of this type is illustrated in Example 6.

×

×

3.2 The interconversion of 1,3Z,5-hexatriene and 1,3-cyclohexadiene

×

The orbital symmetry correlation diagrams for the hexatriene–cyclohexadiene interconversion, a 6π [i.e. a (4n + 2) electron] electrocyclic reaction, show the effects of adding two more electrons to the pericyclic process. In this case it is the thermal process that is disrotatory, while the corresponding photochemical process is conrotatory.